數獨以外的選擇

在課室以外推廣數學，除了課外閱讀（不妨參考方兄的《書海潛遇（數學篇）》），網上也有很多國外的新玩意。

從張博士找到這個譯作「數煩」（Digit Fidget）的遊戲，那是 2000 年美國謎題大賽的作品，簡介如下：

在4x4的１６個方格中，放入從1到9的數字，使其每行每列數字總和，滿足左列與下列的數字，因為只有9個數字但有16個空格，所以有些空格可能沒有數字

我嘗試挑戰入面的例子：


策略上我大致考慮並篩選不同的情況，多少也應用一些基本的數學性質(如最大值、奇數和、偶數和等性質)，第一次試玩花了約半小時，再看看答案，跟在下的答案不同（由第一列起分別是 0905 6008 0407 2130），看來這玩意有機會一題多解。

這裡還有關於該遊戲的策略解說，建議大家試玩後才看。

傳統邏輯玩意

學校剛進入聖誕假期，姑且放下教學的包袱，介紹一些與數學有密切關係的邏輯玩意（其實都是為下月尾的數學賽方特地搜索一些訓練用的題目）。如喜歡進行網上遊戲，相信常見的「渡河問題」如船夫、狼、羊和甘藍菜、3個傳教士和3個土人、五人過橋該不會陌生，但除此之外，不知下面的題目大家又能否嘗試破解？

＝＝＝＝＝＝
甲、乙和丙三人，一人是會計，一人是社工，一人是教師。現在知道丙比教師的年輕齡大，甲和社工不同歲，社工比乙的年齡小。

根據以上條件，試確定他們三人的各自身份。

＝＝＝＝＝＝
某數學競賽中，某校安排四位學生代表。
對其中兩位學生的名次，三位老師作出如下的猜測：

譚老師：「小方第一名，小陳第二名；」
邵老師：「小方第二名，小張第三名；」
李老師：「小明第二名，小張第四名；」

比賽結果公布後，三位教師沒有完全猜中。
每位教師皆只猜中一位學生的名次，另一位的則猜錯了。
問題是，這四位學生的名次如何？（四人名次各不相同）

＝＝＝＝＝＝
挑戰題
（題目源自1981年德國柏林的邏輯思考學院）
有五間房屋排成一列，所有的房屋外表及顏色都不一樣，所有的屋主來自不同的國家，所有屋主都養不同的寵物，喝不同的飲料，抽不同牌子的香煙。

(1) 英國人住在紅色房屋裏。
(2) 瑞典人養了一隻狗。
(3) 丹麥人喝茶。
(4) 綠色的房子在白色房子的左邊。
(5) 綠色房屋的屋主喝咖啡。
(6) 抽Pau Mall香煙的屋主養鳥。
(7) 黃色房屋的屋主抽Dumlinu香煙。
(8) 位於中間房屋的屋主喝牛奶。
(9) 挪威人住在第一間房屋裏。
(10) 抽Blend香煙的人住在養貓人家的隔壁。
(11) 養馬的屋主隔壁住抽Dumlinu香煙的屋主。
(12) 抽Blue Master香煙的房主喝啤酒。
(13) 德國人他抽Prince香煙。
(14) 挪威人住在藍色房子隔壁。
(15) 只喝開水的人家住在抽Blend的隔壁。
(16) 有一個是養兔子的。

請找出什麼國家的人各住什麼顏色的房屋，各養什麼寵物，各喝什麼飲料，及各抽什麼牌子的香煙。

長時間改簿

長時間改簿，對相同的地方出現類似錯誤多少變得麻木，好處是自己的反應也會來得「自然」，順手一揮，加上同一句提醒/評語/督責/安慰，但壞處是自己會不知不覺地忘記，總有人會是很用心去做家課（當然有不少是明顯用心卻明顯一團糟），付上實實在在的光陰，克服打機上網睇電視煲電話粥煲日劇韓劇落旺角上加州窮等等的誘惑（或是克服參加課外活動的魔力），而乖乖地坐在書枱前定睛在一道數學題前費盡心機。

但有時多少也總有感乏力的一刻吧？
畢竟也是人，離開工作間，我也有打盹的時候。

數學•女同學

文：祈思

由數學學會會員名單看見，初中的會員當中，只有四分之一是女同學。這個差異，起初也令我感到驚訝，為什麼學習數學好像有男女之分呢？

一般來說，上數學課時，堂上發言的多數是男同學，計算最快的好像又是男同學，測驗考試最高分數的又是男同學，未知這些是否妨礙女同學學習數學的主因，不過，我認為這個問題很值得關注。

近日有老師指出，理科班女同學的分數偏低，尤其於數學、附加數、物理三方面，男女同學的分數差異更為明顯，中位數以下的多是女同學。理論上，大家的腦袋差不多，不應該有這種分別，我想，導致出現這種情況的原因，是在於外在環境的影響，甚於理解能力。

女同學普遍善於背誦，因此可能會傾向喜歡中文科和生物科；男同學則對電腦、數學、物理充滿興趣，日積月累的知識，形成好像男同學理解偏優的情況，其實，關鍵可能在於興趣。對一門科目有興趣，加上一定的努力，很多時候也可以較一般同學優勢。

我認識一個物理成績很好，但數學成績卻一般的女同學。由於喜歡物理科，平時的功課、習作、堂上發問，對這位女同學來說很容易，考試成績也比許多男同學優勝。可見能否拿到好成績，興趣十分重要。

在整個環境中，女孩總是文靜地聽書，但男孩卻會多發問、思考。女同學不會做物理功課，周遭的同性又不會做，所以可以選擇置諸不理，而沒有壓力；男同學不會做物理功課，卻會拚命地找方法去做，因為四週的男同學都是強者，不會做，顯得過份遜色。數學也如是，當習慣了滿分那個一定是男同學，女同學可能會放棄了爭取，只會留守於成績中等的一群中，最後，又會出現以男同學為主的氣氛。

寫到這裏，忽然想起不同數學老師的話，好像沒有一句是針對性別而說的，他們的話大意都是：「這個世界沒多少個天才，多做、多想才會拿到好成績。」

後記：祈思是某中學數學學會的主席。

一個提問的事後反思

今日放學，有個中二男生走來問我一個問題：

有沒有方法，可以不用計算機，能夠計算出某數的平方根？

其實當下在下正要為手頭上三疊待放的測驗卷煞費苦心，加上睡意正濃，心裡多少有點惰性，不想馬上回答。於是我選了中五的半分法作回應，當他不明白為何要二分的時候，我靈機一動觸跟他玩個「開口中」遊戲，讓其發現拿中間數作試算的技巧，最後借了本「數學拾趣」，著其自行細閱 P.100-103。

當然問題內容還是次要，但所謂「發明千千萬，起點是一問」，我也順道問他發問的動機，他也很坦白回答：「有時我想，如果有日考試欠帶計算機，對住這類題目，能否有解決的方法？」難得的是，他肯主動思考而去發問，事關經驗上，大多數學生寧願想法子提醒自己帶計算機入試場而不會想這個，同時有更大多數人不會如斯細心，都臨場才驚覺漏帶計算機而問你借機，自己心情難免矛盾：「不想借，免得助長歪風，雖知世途險惡，貴人並非必然在左近；想借，始終是自己學生，多少總有點惻隱之心，雖然很想佢死一次...」

其實今時今日，物質生活變得豐富，學生過度依賴計算工具仿佛是大勢所趨，舉例來說，初中數的「科學記數法」，部份程度淺易的題目，其實可透過代入、約簡等代數操作(manipulation)去解決，而不必事事要用計算機代勞。然而，剛剛教授新的課題，學生還未掌握概念本身，便急性問有否用計算機的方法。當然，在下並非一切要返璞歸真，讓學生回到紙算、查對數表的年代，而且投身社會，其實能懂得四則運算、利率應用等可能也都綽綽有餘，不過，這樣的氛圍，恐怕對數學教育多少構成負面影響。恐怕他日連一節數學課，也要加入魔術、笑話、故事的襯托，才或者能夠帶出一點點數學味道。

「科技」、「工具」本身是中性，關鍵在於怎樣運用，但若因著科技而失去那種對數字的觸覺，那比起失去毅力、耐性、嚴謹等態度或共通能力(generic skill)等更是數學教育的不幸。所以習慣上，當學生表示：「其實 XXX 用計算機解決咪可以囉...」我多數也回應一句：「可以用計算機，但又是否必需要用？」

當然，這也是這個部落設立的理念。
希望這裡能成為一個討論數理的選擇。

(繼續回到待改的三疊卷，面對一個個甚有進步空間的學生)

補習成風...

文：祈思

近日，同學們紛紛拿出各補習社的宣傳單張，比量一番。印刷精美奪目的封面，是那些經常於巴士車身、報章雜誌等廣告出現的男女。

標榜著名師指導、奪Ａ必讀的課程，忽然成為學生的靈丹妙藥，彷彿只要補習，就可以令成績突飛猛進。於是，數百元甚至近千元一個月的補習費用，完全不成問題。

補習的成效真的那麼大嗎？學期初，當老師展示出會考成績時，也曾鼓勵大家記得儲好錢，預備日後補習之用。中五的同學也不忘提醒：記得暑假去補好各科！

四周彌漫著趨之若鶩的補習氣氛，可是，一些天才型的學生卻不以為然。他們不用補習，上課時輕輕鬆鬆聽書，筆記也懶得去抄，當老師堂上發問時，卻能十分準確地回答，且以良好的成績遙遙領先。放學後，當別人忙著外出補習時，他們卻可以回家玩電腦或睡覺。

算起來，這麼真的有點不公平！花錢辛苦補習的人不旦不能佔上風，隨著補習時間加長，時間愈來愈少，壓力也愈來愈大，一些突發的集體活動，例如放學後留下做些什麼事時，趕著去補習的人可苦惱了。雖然這樣忙，那樣忙，成績可能只是跟其他學生差不多。

其實，補習像處方藥物一樣，只屬輔助性質。吃完藥後會康復、補過習會維持一定成績，皆是同一道理，只是無形中，家長花的錢多了。但如果把補習看得太重，甚至自以為補過習後就聰慧過人，自嗚得意，那麼只是本末倒置而已。上學時，教師已把重點或概念加以講解，要學的，堂上會教，要不然，教師的存在是為了什麼？難道教科書及不上一本本的精讀筆記？

補習有它的副作用，比方說，當一個學生無法理解抽象的概念時，就會埋怨教師的教學方法，然後乾脆放棄聽書，放正他們留有後著──補習。聽書與否，也就變得無關痛癢。當然，補習也有好處，學校教師無法照顧每一位學生，補習就是多了一個學習的機會，也能從不同角度熟習題目──假如能正確利用的話。

看過相關宣傳小冊子的同學，不久後一踴而至報讀相關課程；不加理會的同學，閒時做做習題，仍能應付自如。至於真正的分別，也許要看年半後的會考成績吧！

兩道關於平方數的證明題

證明以下兩道關於平方數的命題：
（換個比較易明的講法：「點樣先知下面兩句一定啱呢？」）

1. 任何兩個連續單數的積加上１後，答案必然是完全平方數。
2. 任何四個連續數的積加上１後，答案必然是完全平方數。

在不用計算機的情況下，試試如何用代數式表示。

歡迎各方人仕回應。

抄襲家課(1/3)

入職初期，批改課業往往是令自己感到最費時最教人氣餒的地方。尤其是看到一本又一本連字跡也幾乎一模一樣的家課（我稱之為「草書」，字跡凌亂之可怖，至今仍不堪回首），更是教人深感不忿。「幹嗎學生可以草草了事，自己卻要賠上無限青春，去做一些不知意義何在的地方？」

小補充：然而既然我們也會想到「意義」的問題，是故學生也不難會去問「學ＸＸ有什麼用？」、「這樣做有什麼用？」，只是他們需要可以是一些「意義」，而非純粹的工具價值。當然，更大可能性是學生已經悶得不耐煩，才不得有此一問。所以如果學生問起這個，恐怕情況已經是相當嚴重，並非你三言兩語便能解惑，如斯理性的人不多。


人常戲言曰：「天下文章一大抄」，書法中也有所謂「臨摹」，不難發現「依樣畫葫蘆」、「複製」都算是一種學習。但在數學領域，一門講求思考的藝術，身為人師，我們可有怎樣的胸襟去處理這學校常見的「現象」（使用「問題」或「處罰」等字眼恐怕令大家覺得在下視之為負面）？雖作表態，但字眼上我仍想用「抄襲家課」，以方便解讀本文。

對於抄襲家課，我嘗試從犯罪心理學或經濟學的觀點說明一下。

一個人，進行某種選擇的前題是「利益大於代價」（「代價」學術上應稱為期望成本 Expectation/Expected Cost），最常見的例子是囚犯的困境。由此引申，抄襲家課的人便要衡量利益（可能是更快完成家課、和其他靠真材實料的同學取得同樣高分、不被老師打擾或其他...）及代價（壞印象、重做、扣分、寫手冊、家長收到來電/短訊問候、記缺點、留堂或其他...），再考慮被發現/不被發現的機會，繼而進行抉擇。雖然實況告訴我，很多平庸的學生多是只看到利益，也認定被發現的機會接近零，這其實跟一個病態賭徒相信自己有賭未為輸相若，純真得可愛。

也有些深黯以上道理的，便會在抄襲家課的技巧上多花功夫，如抄襲多份家課，以集各家之大成；又或故意製造一些小錯誤，令自己不那麼突出。不過，能夠以批判的思維去辨識哪是小成/大成，能夠分辨對錯以製造一些小錯誤，這些表現多少已經展示其思維能力，只是與我們的價值系統出現差異。

幸好這個世上，並沒有很多夜神月。

暫且想到這裡，事關身為人師，他日當你手上的家課做得很出色，而你卻以「小人之心度君子之腹」的心態去審視這位學生，不是有點兒不公嗎？這裡多少引起「應否信任學生？」的迷思，難免令良知掙扎。至今為止，個人仍相信「信任」是師生關係的支持點，只是這是需要力量及盼望去維持。若有所同感，有時大家還要提防社會上一些「不信任機制」引入學校及自己的思維，幸好考試裡有一條「疑點利益歸於學生」的不成文規定，不然連學校也不能孕育「互信」的種子，這實非我們的領導再引入多少資源便能有所果效。

以下兩個問題，我將會加以評論，有時探索問題的過程比結論更加好玩。
1. 發現「抄襲家課」前，為師可以做什麼？
2. 除選擇「抄襲家課」，學生有什麼其他選擇？

= = = = = = = = = =

"...the kind of thinking that will solve the world's problems will be of a different order to the kind of thinking that created those problems in the first place.(Albert Einstein)"「解答世界的問題所需要的思維，是與產生這些問題的思維，處與不同的層次。」─愛恩斯坦(來源)

一個學數之人的心聲

連結：一個學數之人的心聲

大家認為呢？

只有想不到，沒有做不到的

編課程

來自初中數學科科主任的要求，在下有機會去編訂初中整體的數學課程。雖不如好友兼同行S一年任教中一二三四五的數學科，在下總算對中一二三四數學科也稍有體驗，至少在編排課程時也不至於摸不著頭腦。按照現時所採用的教科書，主要內容合共三十六課，每個學期教六課，就中二數學作為主打，編排如下：

（中一）
有向數
基礎代數
代數式的運算
數型與數列
多項式
統計圖的認識
(下學期)
基礎幾何*
簡單圖形的體積和面積
坐標簡介*
全等與相似三角形
百分法的基本概念
對稱與變換*

（中二）
估算與近似值
公式
多項式
恒等式與因式分解
聯立二元一次方程
統計圖的分析
(下學期)
平面幾何*
面積和體積
畢氏定理
三角比的認識*
全等與相似三角形*
代數不等式

（中三）
指數定律
續因式分解
演繹幾何的初階*
四邊形的特質*
集中趨勢的量度*
概率的認識*
(下學期)
續演繹幾何*
求積法
三角學的應用*
座標幾何*
續百分法
立體圖形的探究

(有*表示會以英語授課)

宏觀角度，課程都是按課題性質作編排。若簡單二分的話，我多數用「煩」及「難」作區分，煩的題目，雖花時間但一般可靠機械化操練去應付：至於難的題目，平日則要多動腦筋，考試中也要花較多時間處理。

課題本身涉及怎麼樣的學習經驗（learning experience）也是重要考慮。例如中二級教授的「面積和體積」、「畢氏定理」、「三角比的認識」裡，學生須學習使用計算機，就是講求精確的運算；另外，以往通常編到最後才教的統計及概率，由於要配合專題研習，課題一律改在上學期末段教授；而為協助學生過渡高中課程，我校所有關於幾何的課程均採用英語授課，務求學生能掌握列寫幾何定理的技巧。

除了考慮所題的先備知識（prior knowledge），也考慮科任教師教學上的預工。比方說，當中一教授「基礎幾何」時，中二級便教授「平面幾何」，而中三則教授「續演繹幾何」，尤其是對任教多於一級的數學教師，此舉有助教師同時檢視學生的學習困難，對教學上可改善的地方，能即時修正及應用在其他課堂之中。若配合課外活動（例如數學學會的相關延伸或增潤活動），相信效果會更顯著。

當然，校本課程編訂多少涉及學校的學習氣氛及教師的數學觀，要達致數學教育專業化，多少均需要前線教師反覆的實證，才能找到有利學生學習的數學課程。

延伸閱讀：數學是甚麼--學生的角度

一點啟發

從學生的分享中，看到這個提問：

一條數學定理，別人窮盡一生研究了些公式、定理出來，目的是給後人知道方便計算，但人們只會覺得複雜、難明，違背了原意，那些哲學家、數學家的一生又算上什麼？

其實，真的算不得甚麼？所謂意義，其實都沒有所謂的定義吧。

一個關於等腰三角形的動畫

何謂等腰三角形


歡迎回應：)

一分(鐘)都不能少

不知大家如何分配課堂時間，如何控制課堂時間，除了是老師本身的功力，也取決於學生的反應。例如面對低學習動機的也有分滋擾性及非滋擾性（後者還「好」，前者分分鐘會使你為之氣結），即使學生積極發問，老師如何就聽到的問題找出背後的意思，也是殊不容易。近年流行的歷奇輔導，當中的解說正正發揮畫龍點睛之效，當然時間管理也不可少。

到底怎樣才可教我們不用來去匆匆？

「是時候回到校園啦...」

由香港教育統籌局資助，為期四星期的數學教師持續發展課程(AA)正式宣告結束。雖然時間倉卒，但就當中有關初中數學的教學心得、課題注意事項、校本評核等，相信參加者相信獲益良多，特此鳴謝香港大學教育學院所有任教教師的啟發及支援。

給我的數學ｍｉｓｓ

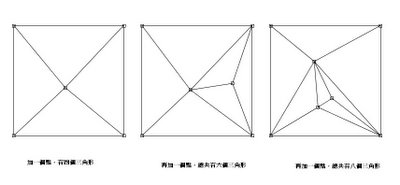
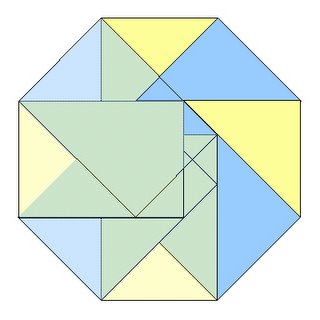
從不相信學習數學是男性的專利（其中一個「原因」，是很多數學老師也是ｍｉｓｓ吧），在三月八日的婦女節，透過以下創作，感謝所有數學ｍｉｓｓ同時，也勉勵所有學生：學習數學，絕非某個性別的專利。
＝＝＝＝＝＝＝＝＝＝
改編歌名：學數驕傲

版本：1.1（更新至23:30，8/3/2006）
原曲：我的驕傲 容祖兒
作曲：陳光榮　　　填詞：黃偉文
編曲：陳光榮　　　監製：陳光榮
改詞：SK@數學真魅

Maths in your mind, 為我改寫下半生
題目裡　找真理　得到的　自銘感
才明白　做算式　能用不一樣法則
榮幸眼神能替我　雲上旅行來點燈

＊See me try, I'm brave to speak my mind
　不因計算煩瑣　只因有妳啟發
　Believe me I can try, I'm proving in the lines
　即使計算無果　因妳教更愉快＊

Maths in your mind, 為我代入像化簡
唯獨妳　欣賞我　比我　更多
埋頭做　願妳可　能為我指示更多
無論有誰嫌棄我　投入卻無人可阻
Repeat＊

我已對公式之變化　著迷　
昂然地對著數字說　是借著妳的恩

Let me try, I'm brave to speak my mind
不因計算煩瑣　只因有妳啟發
Believe me I can try, I'm proving in the lines
假使數有奇蹟　因妳教最愉快
愛數非必然　因有妳　啟發
＝＝＝＝＝＝＝＝＝＝

誠邀各位指點，
望昔日師恩得以傳揚。

柏拉圖立體

在提及一些數學概念，有無感覺，數學老師多是「陳述」而少作「證明」？舉例，要探討以下問題：

為什麼世上只有五個正多面體？

若用傳統的證明，恐怕學生很快便投入周公的懷抱，以下有一個不太嚴謹的「解釋」，希望讓大家知道，其實除了傳統的證明，我們也可有其他出路。

想想，...

要將幾個正多面體正多邊形「拍埋」一齊...
1. 每個頂點(vertex)至少要由三個面組成
2. 多邊形聚於一頂點的內角總和不能等同或超過360度

再考慮正多面體每角內角：等邊三角形(60度)、正四邊形(90度)、正五邊形(108度)、正六邊形(120度)...，但由正六邊形開始已不能砌成立體(為什麼？)，所以可以肯定

正多面體的每一個頂點只可以由等邊三角形、正四邊形、正五邊形形成

再考慮上面條件1

考慮由3個等邊三角形組成的頂點(正四面體)
考慮由4個等邊三角形組成的頂點(正八面體)
考慮由5個等邊三角形組成的頂點(正二十面體)
考慮由6個等邊三角形組成的頂點(不行啊~)
考慮由3個等邊四角形組成的頂點(正六面體)
考慮由4等邊四角形組成的頂點(不行啊~)
等等...

如此類推(嘗試自行查考吧)，相信大家應該接受上面的提問吧

延伸閱讀：教育城 簡報庫 鄭禮林老師的教學簡報、伍達洋老師的工藝作品，摺紙正多面體，李栢良先生的介紹

淺談數學思考方法

每年入到三月，學界一連串數學競賽也進入白熱化階段。作為數學老師，除了平日處理課室教學，面對社會各方面合理及不合理的要求，今云特地以培正中學數學邀請賽為例，淺談初中常用的數學思考方法（如使用中大出版社《ｘｘ新里程》的學校，課本第０課應該有介紹）。

以第一屆的數學邀請賽個人賽(中三組)題目為例，在90分鐘內，參賽者要完成合共20條題目，而2分題、4分題、6分題、8分題的題目各佔5條，即是說，若按比例以分數分配作答時間的話，參賽者每部份的時限為9分鐘、18分鐘、27分鐘、36分鐘。好不容易唷～

今云，在下選了一道6分題及8分題作介紹。

Q14. 在一個正方形內畫2002個點，並把其中一些點用線段連起，再沿這些線段把正方形切割成一些三角形，而這些三角形的頂點均為正方形的頂點或該2002點中的一些點。問最多可得多少個三角形？

（6分題目，即你只可用大約五分鐘完成哩！）
首先留意題目中「2002」這個數字是否必須，否則大家不妨考慮「正方形內畫1個點」的情況，再考慮「正方形內畫2個點」的情況，如此類推，看看能否找到答案（見附圖）

重點：簡化問題，從中尋找規律（simplication  pattern generation）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝


「傳統」上，圖中你可以找出一些相似三角形，再用方程找到答案。反正一般初中生只學了平行線、全等、相似之類的概念，大柢錯不了。

不過今云在下介紹圖解法。但如果閣下不黯使用圓規直尺，以下的提示不看也罷。

1. 考慮問題的附圖，利用圖規依次畫紅色三角形BCD及藍色三角形BAE。
2. 分別以A、B為圓心，分別作圓，兩者相交於F。
3. 連上CF(下圖為參考)。

反正參加數學比賽和老試不同，能找到答案。有空的話，拿這個作飯後果也倒不錯呢。

重點：善用畫圖，直接量度。

歡迎回應或轉載：)



延伸閱讀：香港培正中學數學邀請賽、第一屆數學邀請賽(2002年) 個人賽(中三組)題目


挑戰題：
董先生參加某國家的總統選舉，
得票率(準確至小數點後一個位)為66.6%，
問董先生至少得幾多票？

(來源：第一屆數學邀請賽中三組個人賽第19題)

想當年，大家怎樣學「指數定律」？

課堂解構

在一個有關數學的研討會，有學者指出：

研究所得，以一堂五十分鐘的數學課為例，香港的數學老師總共講了 5798 個字；而比較老師及學生的說話比例，香港教師每講16個字，學生才開口講1個字(日本的比例是13:1；美國的比例是8:1)...

不妨檢視一下，我們一節的數學課裡，以下活動的時間分配是怎麼樣呢？理想的時間分配應該怎樣？實際上又有什麼限制？

• 學生獨自做習題(彼此不加以干擾)
• 小組協作做習題
• 老師講講講...
• 學生做發表做匯報
• 訓育？
• 輔導？
• 其他

說到底，我們是否提供足夠的機會讓學生建立數學的概念？

估，都要估得有個譜吧？

（午飯後上數學堂，「飯氣」正遊走經絡之間．．．）
「ｘ同學，若你用估算，你估一架巴士太約有幾高啊？」
「．．．er．．．咪大約．．．大約高廿米啦～」

這些反智思考不夠慎密的應對，相信大家不會感到陌生。
以下的活動，希望令大家有所啟發。

活動推介：金字塔的估算活動

1. 輸入以下網址：http://www.ancientegypt.co.uk/pyramids/activity/main.html
2. 分別就高度、底面積、重量進行估算。
3. 提醒學生自行寫下，暫時不作任何討論。(避免學生受他人影響)
4. 過程中的提問...「有什麼解題策略？」「有無其他特別的考慮？」
5. 就學生的解釋加以補充。
6. 輸入其中一個「較合理」的學生答案（應該無可能估中，但這不打緊），讓學生再估／公佈答案。

雖然這不是關於數學教育，但過程中我們可了解學生對想像與真實之間的差別。另外每個處境「估」的成份各有不同，教師可加以比較讓學生知道：「估，都可以估得有個譜吧。」

延伸活動： 電子間尺、動畫及使用介紹（英）

一點想法：教學重點不在於學生是否「估中」（結果），而是讓學生了解自己及其他人怎樣估算（過程）

歡迎回應：)

求積法的提問 Questioning in Measuration

有人認為，對面積公式，應該要等一定要記熟，有些最好能背誦，朗朗上口。然而，好的提問，除了能啟發思考，其實對協助學生如何組織概念起重大作用。即使要背，也應該要背得有系統吧？


(在黑板上畫上附圖)

問：三角形面積的大小和「底」、「高」有什麼關係？
問：如果三角形的底／高不變，三角形面積的大小和高／底有什麼關係？
問：兩個完全一樣的三角形可以拼成一個已學過的什麼圖形？
問：拼成的圖形的底是原來三角形的哪一條邊？
問：拼成的圖形的高是原來三角形的什麼？
問：三角形的面積是拼成的圖形面積的多少？
問：怎樣來表示三角形面積的計算公式？
問：為什麼求三角形面積要用底乘以高再除以2？
問：如何解釋為何三角形、梯形的面積公式均有二份之一？
問：你能利用梯形面積公式，推導其他圖形的面積公式嗎？
問：如果只可以背熟一條公方式，你會如何選擇？
問：形式上，這些公式有什麼相似的地方？

延伸閱讀：數學課的提問藝術

錯在哪裡？

在一個數學比賽中找到這條數學題，對錯都是其次，怎樣理解，其實比知道答案更加有價值。
(數據顯示，有五份之一同學根據附圖作答，人數比答對的人更多)
問：學生是怎樣理解呢？

歡迎回應：)

[轉載+精華] 數學文字題及課業的處境應該有多真實？

作者：黃家鳴(香港中文大學課程與教學學系)

完全脫離日常生活實際的數學難題又是否完全不可取呢？

一位心理學家問小孩：「如果你到雜貨店買糖果，值6仙，你付了10仙，應找回零錢多少？」小孩答他從未擁有過10仙，如果有，他絕不會拿來買糖果，況且他媽媽也會做糖果。

類似趣事其實來自一本三十年代的教育心理學著作，聽起來並不陌生，或者我們小時候也曾被人問過類似的問題，諸如樹上有10隻小鳥，獵人瞄準了1隻並開槍打牠下來，問樹上還有小鳥若干。如果你正經八百地計算10減1的話一定讓出題的人笑得人仰馬翻。

那麼數學課是否真的有些什麼特別，以致學生「懂得」以另外一種方式、態度來處理數學課涉及的問題呢？…這裡我們隱約見到當問題的真實性較高時，學生還是會考慮一些現實需要和條件的。

其他要點：

• 有趣的處境難題可以提高學習興趣，但要認真思考如何避免太多太人工化的虛擬處境。

• 其實，數學以其純粹形式出現的很多情境都足以令不少學生傾心而沉醉於解題之中，問題反而是數學教師本身的數學素養，是否足以支撐一個有數學味道的數學課。
  

…
最後，僅以一題完全虛假卻不能不如此擬題的文字題作結：

保羅放下他的書，在一張小紙片上計算著。
「這本書裡有很多可讀的東西，」他告訴他的妻子，「我想你也一定喜歡。」
不要讓我等太長時間！」瓊微笑說，「你還有多少要讀？」「將近150頁，」保羅回答道，「我看這裡有些東西非常奇特。第一章是從第13頁開始的，從這一頁到我現在正看著的前一頁，那些頁的頁數相加，跟我將要看的那些頁的頁數相加，兩者和是一樣的。」「那麼你看的時候有沒有跳過一些頁呢？」瓊問，「無論如何你等看完書再去算那些東西，我想要書！」實際上保羅一頁都沒有跳過。

試問，他手頭正在讀的是第幾頁？

延伸閱讀：原文(須另轉簡體字)及<數學教育>

空間與量度

從友基部落看到google earth的免費下載及介紹，當中也想到一些教學上的提問：

Q1：找出一所學校的所在點，估算學校操場的大小。
Q2：事前試找出美國五角大廈、羅馬競技場、北京的故宮，請學生探討箇中的形狀。
Q3：就一城市的街道圖，形容這些形狀的數學特性。

當然，這些軟件是工具，提出什麼問題也是其次，更重要的是教師本身要掌握課堂的目標，如何緊扣內容的要點，同時盡量避免自己及學生偏離主題。

如果由閣下任教，你可想到什麼有意義的數學課？歡迎指教及回應。

用英語讀數學符號

考慮到有中中學校於高中改以英語授課，希望這個網址對大家有用。

來源：順德聯誼總會鄭裕彤中學-數學科

[代數]第一次的數學危機的啟思

(轉載自數學資料庫中的數學漫畫)

與其直接陳述當中的來龍去脈，這裡有個活動建議：將八張A4紙鋪成下列的圖樣，探討A4紙長和闊的關係。再考慮使用其他長和闊均為整數的矩形，看看能否做到圖中的效果。


對於活動，個人愚見還是要先看學生是否合作，不然，留下網址讓學生自行了解吧。

從七個圓學習平面圖形

Q1：怎樣利用微軟的Word繪畫以上圖形？
L：先畫一個圓形，選擇[複製]+[貼上]作第二個相同大小的圓。將兩個圓剛好成八字形後，選擇[群組]後，再用[複製]+[貼上]作另外兩組八字形，移庢重疊後，分別旋轉60度及120度。最後在圖中央貼上最初的圓形，完成。

Q2：根據圖中的相交點，可連結成多少種四邊形？試繪製表示。

Q3：根據繪製的四邊形，試計算每個內角的大小。

Q4：根據圖中的相交點，可連結成多少種矩形？試繪製表示。

Q5：根據繪製的矩形，哪些具相似的性質？試解釋說明。


以上問題，歡迎提出意見。(請註明所回答的問題)