三角形的心、歐拉線、歐拉圓、費馬點

看本文前，先到此連結玩玩啦~

以下是我很喜歡的自學教材(一)、教材(二)，若在課室使用投影機，請確保房間夠暗唷。

此外，對任意三角形，
「三邊的中點」、「三條高線的垂足」及「垂心和三頂點連線的中點」，這九點共圓，這個圓稱為 "九點圓" ，且其半徑為 ½ R (R 為三角形外接圓的半徑)。九點圓亦叫做 :
歐拉圓 (Euler Circle) < 我較喜歡的稱呼~ 龐斯萊圓 (Poncelet Circle) 費爾巴哈圓 (Feuerbach Circle)

此外，不得不提的還有費瑪點(Fermat Point)，費馬(Pierre de Fermat,1601-1665)本身是一名律師，數學是其業餘的嗜好，話雖如此，他在數學上的成就不比職業數學家差，雖則無「發表」論文，但是他幾乎與同期所有歐洲大數學家保持通信。話說他收到一個問題：

要找出三角形裡最小點的位置，
這個最小點是指這點到三個頂點的距離總和為最短。

套用今日的情況，如果 M 記要開分店，讓這分店到這三個屋苑(A,B,C)的距離總和是最短，那麼這個位置(F)就叫做費馬點。它的「作圖法」及「幾何證明」是吸引我的地方。

幾何證明本身分2個情況：
(1)三角形全部內角內角都小於120^o　
(2)三角形其中一隻內角不小於120^o
記得以前初初接觸該題目，我竟意想不到情況(2)的出現...Orz

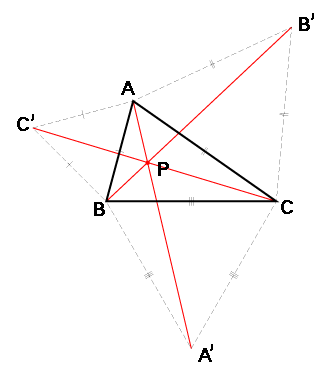
根據情況(1)，用規尺作圖的技巧，
按三角形的邊長作三個等邊三角形。
連接 CC'、BB'、AA'，
則三條線段的交點就是所求的點。

證明步驟
(1)證明 CC'、BB'、AA'三線共點(collinearity)
(2)證明P點的唯一性(uniqueness)
可惜的是，我所用的步驟涉及圓形的定理，若以初中生作對象，使其明白三線共點的證明應十分費時。課時內不易處理（外心、內心、垂心、重心其實也涉及三線共點，但在下即使任教「精英班」，觀其反應，都只能輕輕帶過 Orz），諸位若有什麼更好的視覺證明(visual proof)，請不吝賜教。

教師延伸閱讀：尋找費馬點：從一道數學應用問題談起

球體體積公式 Derivation of formula of volume of sphere

前言：打從香港中文大學黃毅英老師知悉，重開的數學教育學士課程收了近 40 位本科生，能夠招聚這麼多有心人，我也重燃寫文的動力，今次選擇更新一篇三年前的文章，希望給有心人多一個教材選擇。

「如何『證明』球體相關公式？」(來源)



在前線打滾一段時間，四年前已發現不少學生寧可選擇背誦而不太願意深究。不只是能力或動機稍遜的同學，就連所謂尖子也抱這種心態。要稍為深入認識這漂亮的證明過程當真如此遙不可及？下面是一個 Sketchpad 檔，檔案精采地方是能夠調校高度展示不同位置的切面，另外我嘗試轉用 Powerpoint 放在堂上分享（少了些互動成分），但都希望幫到學生有進一步探究。







或者...







延伸閱讀

自製教具驗證球體表面面積及體積公式

阿基米德的數學成就和研究方法



學術文章

A Fresh Look at the Method of Archimedes